Graph
Data structures used to represent Graph:
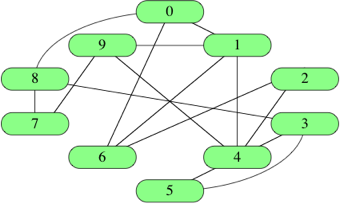
It is common to identify vertices not by name (such as "Audrey," "Boston," or "sweater") but instead by a number. That is, we typically number the |V| vertices from 0 to |V|-1. Here's the social network graph with its 10 vertices identified by numbers rather than names:
Adjacent Matrix
Adjacent List
Edge List
Check if graph has cycle
- For Undirected Graph, We can use
DFSorUnion Findapproaches.
DFS
public class Graph{
private int V; //vertice index
private ArrayList[] adj;//adjacency list
Graph(int v){
this.V=v;
adj=new ArrayList[v];
for(int i=0;i<v;i++) adj[i]=new ArrayList();
}
void addEdge(int v, int w){
adj[v].add(w);
adj[w].add(v);
}
boolean hasCycle(){
boolean[] visited=new boolean[V];
for(int i=0;i<V;i++){
if(!visited[i]){
if(hasCycleFun(i,visited,-1)) return true;
}
}
return false;
}
boolean hasCycleFun(int v, boolean[] visited, int parent){
visited[v]=true;
Integer i;
Iterator<Integer> iterator=adj[v].iterator();
while(iterator.hasNext()){
i=iterator.next();
//if adjacent vertice is not visited
if(!visited[i]){
if(hasCycleFun(i,visited,v)) return true;
}else{//if visited, it should be it's parent, otherwise there is a cycle
if(i!=parent) return true;
}
}
return false;
}
// Test function
public static void main(String args[])
{
/* Create a graph given in the above diagram
1---0--3--4
\ /
2
*/
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
if (g1.hasCycle())
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't contains cycle");
Graph g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
if (g2.hasCycle())
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't contains cycle");
}
}
Union Find
Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether the graph has cycle (or these edges make up a valid tree).
Note: this requires that no duplicate edge presented
public boolean hasCycle (int n, int[][] edges) {
if(n<=1) return true;
int[] parent=new int[n];
for(int i=0;i<n;i++) parent[i]=i;
for(int[] edge: edges){
int l=findroot(parent,edge[0]);
int r=findroot(parent,edge[1]);
if(l==r) return true;
parent[l]=r;
}
return false;
}
public int findroot(int[] parent, int i){
while(parent[i]!=i){
parent[i]=parent[parent[i]];
i=parent[i];
}
return i;
}
- For directed Graph, use
DFSapproach.
Directed Acyclic Graph (DAG) is a finite directed graph with no directed cycles. That is, it consists of finitely many vertices and edges, with each edge directed from one vertex to another, such that there is no way to start at any vertex v and follow a consistently-directed sequence of edges that eventually loops back to v again.
Equivalently, a DAG is a directed graph that has a topological ordering, a sequence of the vertices such that every edge is directed from earlier to later in the sequence.
Analysis:
We will start from node that is of 0 indegree, apply depth first search to check for all the path and see if there is a cycle.
Also we can use
Topological Sortingmethod to see if the graph has a topological ordering.
public class Graph{
private int V; //vertex number, size of Graph
private ArrayList[] adj;//directed adjacency list
Graph(int v){
this.V=v;
adj=new ArrayList[v];
for(int i=0;i<v; i++) adj[i]=new ArrayList();
}
void addEdge(int v, int w){//directed: v-->w
adj[v].add(w);
}
boolean hasCycle(){
boolean[] checked=new boolean[V];
boolean[] visited=new boolean[V];
for(int i=0; i<V; i++){
if(!checked[i]) {
if(hasCycleFun(i, visited, checked)) return true;
}
}
return false;
}
boolean hasCycleFun(int v, boolean[] visited, boolean[]checked){
//if next vertice visited, there should be a cycle
checked[v]=true;
if(visited[v]) return true;
//else, check all the next directed adjacent vertice
visited[v]=true;
Integer i;
Iterator<Integer> iterator=adj[v].iterator();
while(iterator.hasNext()){
i=iterator.next();
if(hasCycleFun(i, visited, checked)) return true;
}
visited[v]=false;
return false;
}
// Test function
public static void main(String args[])
{
/* Create a graph given in the above diagram
0----->2-->3<--4
^ |
| |
--1<--
*/
Graph g1 = new Graph(7);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 3);
g1.addEdge(4, 3);
g1.addEdge(5, 3);
g1.addEdge(6, 3);
if (g1.hasCycle())
System.out.println("Graph contains cycle");
else
System.out.println("Graph doesn't contains cycle");
}
}
Check if Graph is a valid Tree
For a directed graph:
1. Start from the vertex of 0 indegree (if there is more than one or no such vertex, fail).
2. Do a BFS. If you encounter an already visited vertex, it's not a tree.
3. If you're done and there are vertices left, it's not a tree - the graph is not connected.
4. To check for a binary tree, additionally just check if each vertex has at most 2 outgoing edges.
For an undirected graph, you can simply check for a cycle with a simple depth-first search:
"Any connected Graph without a cycle is a Tree"
Topological Sort
a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.
Kahn's Algorithm
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)