Hanoi Tower

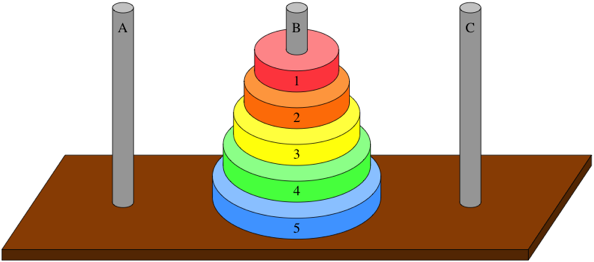
You are given a set of three pegs and n disks, with each disk a different size. Let's name the pegs A, B, and C, and let's number the disks from 1, the smallest disk, to n, the largest disk. At the outset, all n disks are on peg A, in order of decreasing size from bottom to top, so that disk n is on the bottom and disk 1 is on the top. Here's what the Towers of Hanoi looks like for n = 5 disks:

The goal is to move all n disks from peg A to peg B:

Analysis:

While, this is a representative recursive problem.

To move n disks from peg A to peg B.

1.We can move the top n-1 disks from peg A to peg C first.

2.Then move the bottom one from A to B. Then move all the n-1 disks from peg C to peg B.

Solution:

public class HanoiTower(){
    class Tower{
        private Stack<Integer> disks;
        private int index;
        public Tower(int i){
            disks=new Stack<Integer>();
            index=i;
        }

        public int index(){
            return index;
        }

        public void add(int d){
            if(!disks.isEmpty() && disks.peek() <=d) System.out.println("Error placing disk"+d);
            else                                     disks.push(d);

        }

        public void moveTopto(Tower t){
            int top=disks.pop();
            t.add(top);
            System.out.println("Move disk"+ top + "from"+index() + "to"+ t.index());
        }

        public void print(){
            System.out.println("Contents of Tower" + index());
            for(int i=disks.size()-1;i>=0;i--) 
                System.out.println(" "+disks.get(i));
        }

        public void moveDisks(int n, Tower destination, Tower buffer){
            if(n>0){
                moveDisks(n-1, buffer, destination);
                moveTopto(destination);
                buffer.moveDisks(n-1, destination, this);
            }
        }
    }

    public static void main(String[] args){
        int n=N;
        Tower[] tower=new Tower[3];
        for(int i=0;i<3;i++) tower[i]=new Tower(i);

        for(int i=n-1;i>=0;i--) tower[0].add(i);

        tower[0].moveDisks(n, tower[2],tower[1]);
    }
}